Ex 1.5 Class 9 Maths Question 1.
Classify the following numbers as rational or irrational.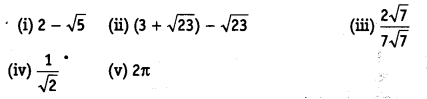
Solution:
(i) Since, it is a difference of a rational and an irrational number.
∴ 2 – √5 is an irrational number.
(ii) 3 +
which is a rational number.
(iii) Since,
(iv) ∵ The quotient of rational and irrational number is an irrational number.
∴
(v) ∵ 2π = 2 x π = Product of a rational and an irrational number is an irrational number.
∴ 2π is an irrational number.
Ex 1.5 Class 9 Maths Question 2.
Simplify each of the following expressions
Solution:
(i) (3 + √3)(2 + √2)
= 2(3 + √3) + √2(3 + √3)
= 6 + 2√3 + 3√2 + √6
Thus, (3 + √3)(2 + √2) = 6 + 2√3 + 3√2 + √6
(ii) (3 + √3)(3 – √3) = (3)2 – (√3)2
= 9 – 3 = 6
Thus, (3 + √3)(3 – √3) = 6
(iii) (√5 + √2)2 = (√5)2 + (√2)2 + 2(√5)(√2)
= 5 + 2 + 2√10 = 7 + 2√10
Thus, (√5 + √2 )2 = 7 + 2√10
(iv) (√5 – √2)(√5 + √2) = (√5)2 – (√2)2 = 5 – 2 = 3
Thus, (√5 – √2) (√5 + √2) = 3
Ex 1.5 Class 9 Maths Question 3.
Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is π =
Solution:
When we measure the length of a line with a scale or with any other device, we only get an approximate ational value, i.e. c and d both are irrational.
∴
Thus, there is no contradiction in saying that it is irrational.
Ex 1.5 Class 9 Maths Question 4.
Represent
Solution:
Draw a line segment AB = 9.3 units and extend it to C such that BC = 1 unit.
Find mid point of AC and mark it as O.
Draw a semicircle taking O as centre and AO as radius. Draw BD ⊥ AC.
Draw an arc taking B as centre and BD as radius meeting AC produced at E such that BE = BD = 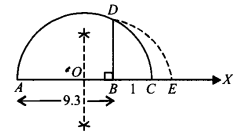
Ex 1.5 Class 9 Maths Question 5.
Rationalise the denominator of the following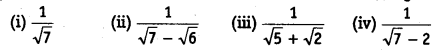
Solution: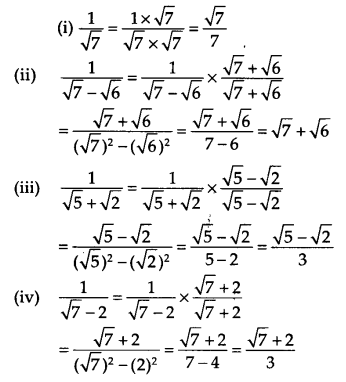







0 Comments
Please comment here if you have any queries or any problems.