Question 1.
Find the remainder when x3 + 3x2 + 3x + 1 is divided by
(i) x + 1
(ii) x –
(iii) x
(iv) x + π
(v) 5 + 2x
Solution:
Let p(x) = x3 + 3x2 + 3x +1
(i) The zero of x + 1 is -1.
∴ p(-1) = (-1)3 + 3(-1)2 + 3(-1) +1
= -1 + 3- 3 + 1 = 0
Thus, the required remainder = 0
(ii) The zero of 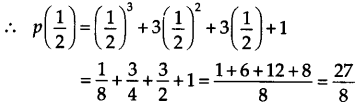
Thus, the required remainder =
(iii) The zero of x is 0.
∴ p(0) = (0)3 + 3(0)2 + 3(0) + 1
= 0 + 0 + 0 + 1 = 1
Thus, the required remainder = 1.
(iv) The zero of x + π is -π.
p(-π) = (-π)3 + 3(- π)22 + 3(- π) +1
= -π3 + 3π2 + (-3π) + 1
= – π3 + 3π2 – 3π +1
Thus, the required remainder is -π3 + 3π2 – 3π+1.
(v) The zero of 5 + 2x is 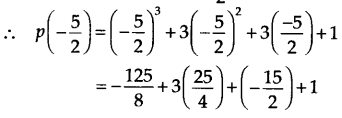
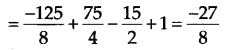
Thus, the required remainder is
Question 2.
Find the remainder when x3 – ax2 + 6x – a is divided by x – a.
Solution:
We have, p(x) = x3 – ax2 + 6x – a and zero of x – a is a.
∴ p(a) = (a)3 – a(a)2 + 6(a) – a
= a3 – a3 + 6a – a = 5a
Thus, the required remainder is 5a.
Question 3.
Check whether 7 + 3x is a factor of 3x3+7x.
Solution:
We have, p(x) = 3x3+7x. and zero of 7 + 3x is 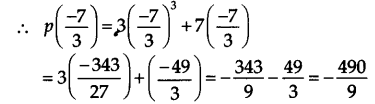
Since,(
i.e. the remainder is not 0.
∴ 3x3 + 7x is not divisib1e by 7 + 3x.
Thus, 7 + 3x is not a factor of 3x3 + 7x.







0 Comments
Please comment here if you have any queries or any problems.